Generative kumiko geometry
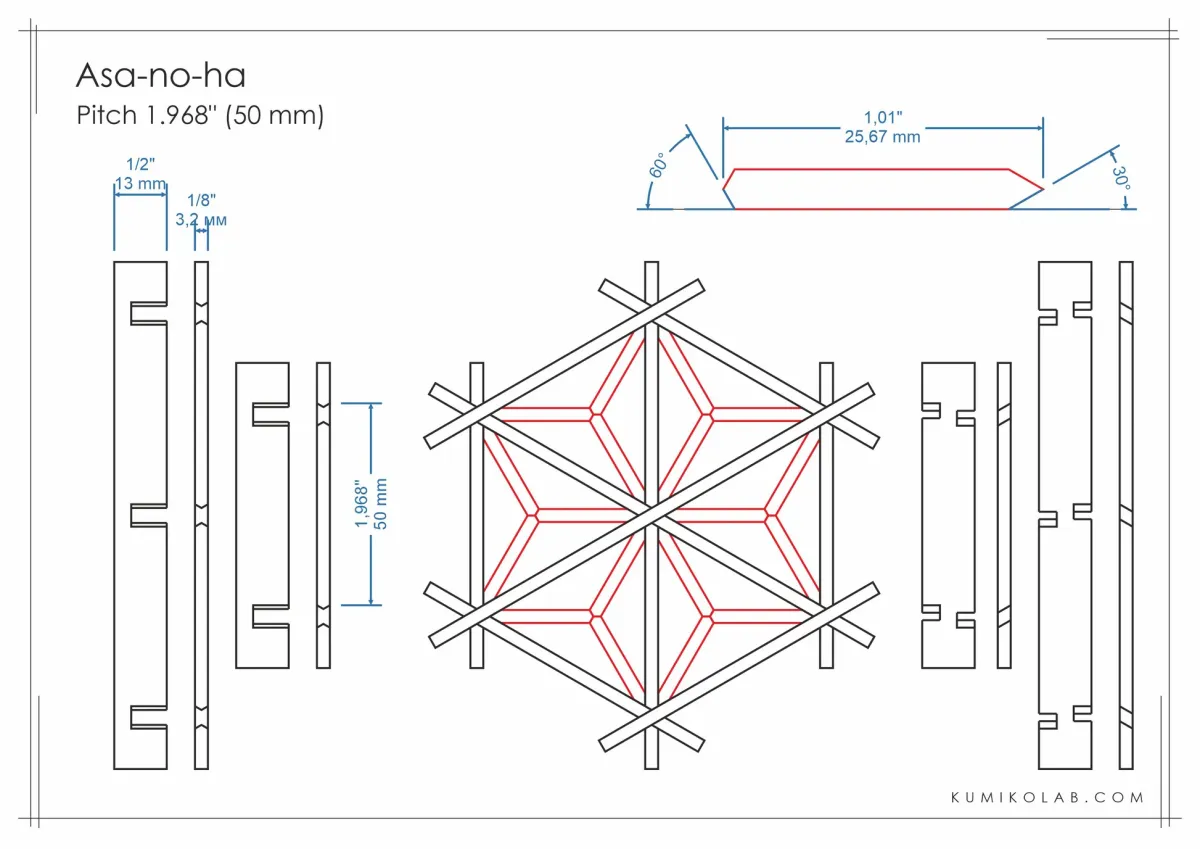
I implemented 24 distinct Kumiko patterns (Asanoha, Kagome, Shippo, etc.)
Kumiko is a traditional Japanese woodworking technique where thin wooden pieces are fitted into intricate lattice patterns without nails. The results are stunning: geometric symmetry, light, and shadow blending into something more than the sum of its parts.
I was inspired by this custom lamp while on a trip in Japan
My goal: animate these transformations smoothly while maintaining the aesthetic integrity of the original craft.
A geometry problem
The foundation is a hexagonal grid. Not squares - hexagons. This immediately introduces interesting challenges:
- Hex vertices are calculated using
r * cos(π/3 * i + π/6)for 6-fold rotational symmetry - Tiling requires offset rows: every other row shifts by
√3 * r / 2 - Edge cases matter: hexagons need neighbors outside the visible canvas to show complete connection patterns
I implemented 24 distinct Kumiko patterns (Asanoha, Kagome, Shippo, etc.), each defined by how vertex endpoints interpolate between the hexagon center and adjacent vertices. The magic happens in continuous morphing between these states.
Beyond simple interpolation
A conversation with jarmani led me down an interesting tangent into Superellipses (Lamé curves) and the Superformula, both capable of generating organic, symmetric shapes by varying exponential parameters. The Superformula, in particular:
r(θ) = [|cos(m*θ/4)/a|^n2 + |sin(m*θ/4)/b|^n3]^(-1/n1)This could generate everything from circles to stars to complex flowers by tweaking m, n1, n2, n3. While I didn't implement it here (the Kumiko patterns are traditionally rigid geometric forms), it's a fascinating direction for future experimentation - imagine morphing between Kumiko patterns and organic superformula shapes.
Initial implementation? Charming but sluggish at ~30 FPS. After profiling:
Pre-computation wins:
- Cached trigonometric values at class level (cos/sin for hex vertices)
- Pre-rendered gradient background as a surface (major gain - no more drawing 700+ lines per frame)
- Used bit shifts for multiplication by 2:
HEX_RADIUS << 1
Anti-aliasing the hard way: Since Pygame's aaline() fails on thick lines, I built custom anti-aliased rendering using pygame.gfxdraw, drawing lines as filled polygons with rounded end caps:
Result: Smooth, non-pixelated lines at any thickness, running at solid 60 FPS.
The trickiest part was ensuring seamless looping. Linear interpolation between states caused visual "pauses" at transition boundaries. Solution:
- Calculate transition duration based on geometric distance traveled
- Use sawtooth wave progression (always forward, never reverse)
- Duplicate first state at end of array for wrap-around smoothness
The Result
A hypnotic, continuously morphing display of 24 traditional Kumiko patterns, each flowing into the next with perfect geometric precision. The code is clean, performant, and extensible - adding new patterns is just a matter of defining endpoint interpolation rules.
Next experiments: Integrating the Superformula for hybrid organic-geometric transitions.
Sometimes the best weekend projects come from just asking: "I wonder if I could code that?"